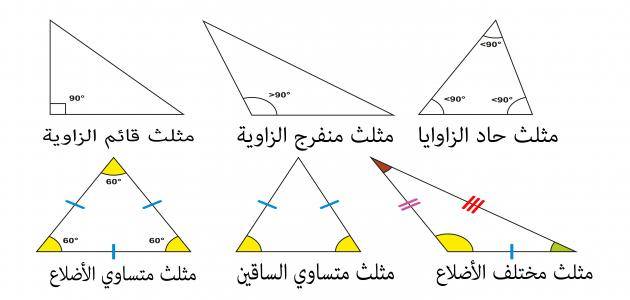
إن من أجل معرفة كيفية حساب محيط المثلث متساوي الساقين فيجب أن نعرف ما هو المثلث متساوي الساقين وما هي شروط تكونه. يسمى المثلث متساوي الساقين إذا كان له أي ضلعين متساويين. كما تكون الزوايا المقابلة لهذه الأضلاع المتساوية؛ متساوية بدورها أيضًا. لذلك فإن النظرية التي تمثل وتصف المثلث متساوي الساقين هي أنه إذا كان المثلث له ضلعان متطابقان، فإن الزوايتين المقابلتين لهذين الضلعين متطابقتان.
كيفية حساب محيط المثلث متساوي الساقين
المثلث هو مضلع له ثلاثة أضلاع حيث يمكننا تعريفه على أنه شكل محصور أو محاط بثلاثة مقاطع سطرية. لذلك يمكن اعتباره أنه أصغر مضلع ويكون له ثلاثة أضلاع وثلاثة رؤوس. وبناءً على قياس طول الأضلاع، يمكننا تصنيف المثلث على أنه متساوي الأضلاع أو متساوي الساقين أو متدرج أي أن جميع جوانبه غير متساوية. والمثلث متساوي الساقين يكون له أي ضلعين من أضلاعه الثلاثة متساويين. كما تكون الزوايتان المتقابلتان للضلعين المتساويين متطابقتين. بالتالي يتم تحديد المثلث متساوي الساقين من خلال زاويتين أساسيتين متساويتين في النسبة أو متطابقتين.
قد يهمك أيضًا: بكم ضعف يزيد المتر الواحد عن السنتيمتر الواحد
ما هو محيط المثلث
قد يهمك أيضًا: وحدة لقياس الطول يشيع استخدامها لقياس طول بعض الاجهزة من اربع حروف
من أجل أن نعرف كيفية حساب محيط المثلث متساوي الساقين علينا أن نفهم أولاً ما هو محيط المثلث. إن كلمة المحيط “Perimeter” مأخوذة في الأساس من الكلمة اليونانية “peri” التي تعني “حول”، وكلمة “metron” التي تعني قياس. لذلك يعرف الطول الإجمال لحواف أي شكل بالمحيط، بالتالي فإن المحيط هو مجموع طول ضلوع أي مضلع. وذلك يسري على أي شكل مغلق. أما بالنسبة للمثلثاث فيمكننا حساب محيطها من خلال جمع أطوال أضلاعها الثلاثة. فإذا كان للمثلث ثلاثة جوانب هم أ، ب، ج، فإن محيط المثلث يمكن تمثيله بالقانون التالي حيث ح تشير إلى المحيط:
- ح = (أ + ب + ج)
صيغة المحيط الخاص بالمثلث متساوي الساقين
محيط المثلث متساوي الساقين هو مجموع أطوال أضلاعه. وبما أن المثلث متساوي الساقين له ضلعان متطابقان، فإن المحيط يساوي مجموع ضعف طول الأضلاع المتساوية زائد طول الضلع الآخر. ويمكن قياس المحيط بوحدات مثل المليمترات (مم) والبوصات (بوصة) والسنتيمترات (سم) والأمتار (م) وهكذا. فإذا كان المثلث له ضلعين متساويان هما أ، أ وكانت ب هي قاعدة المثلث متساوي الساقين فإن قانون حساب المحيط يكون كالتالي:
- ح = (أ + أ + ب) = (2 أ + ب)
قد يهمك أيضًا: المنشور الثلاثي له كم حرف
أمثلة وتطبيق على قانون المحيط
قد يهمك أيضًا: كيفية حساب مساحة قطعة أرض
- س 1. احسب محيط مثلث متساوي الساقين قاعدته 6 سم وأضلاعه المتساوية 5 سم.
الإجابة: إذا كان طول الأضلاع المتساوية 5 سم والقاعدة 3 سم. وإذا كان أ، أ ضلعان متساويين 5 سم وقاعدة المثلث 6 سم. فإن المحيط = (2 أ + ب). إذن ح = (2 × 5) + 6 = 10 + 6 = 16 سم.
- س 2. احسب قاعدة مثلث متساوي الساقين محيطه 30 سم وأضلاعه المتساوية 8 سم.
الإجابة: إذا كان أ، أ ضلعان متساويين و ب قاعدة المثلث متساوي الساقين ومحيطه 30 سم، فبالتعويض في قانون المحيط ح = 2 أ + ب يكون القانون كالتالي : (2 × 8) + ب = 30 سم أي أن 16 + ب = 30 سم. لذلك يكون طول القاعدة ب = 30 – 16 = 14 سم. إذن قاعدة المثلث المتساوي الساقان تساوي 14 سم.
- س 3. إذا كان طول قاعدة مثلث متساوي الساقين 10 سم والمحيط يساوي 40 سم، أوجد طول الضلعين الآخرين.
الإجابة: إذا كان أ، أ ضلعان متساويين و ب قاعدة المثلث متساوي الساقين فإن محيطه ح = 2 أ + ب. والآن بالتعويض في ب = 10 فإن 2 أ + 10 = 40، من ثم 40 – 10 = 30. لذلك فإن 2 أ = 30 أي أن أ = 15 سم وهو طول الضلعين المتساويين في المثلث.
قد يهمك أيضًا: كيف احسب المتوسط الحسابي
ملاحظات هامة عند حساب محيط المثلث المتساوي الساقين
- يعتبر المثلث متساوي الساقين إذا كان له ضلعان فقط متساويان.
- بما أن المثلث متساوي الساقين له ضلعان متساويان، فيمكن حساب محيطه إذا كانت القاعدة والأضلاع المتساوية معروفة.
- صيغة قاعدة أو قانون حساب محيط المثلث متساوي الساقين هي ح = (2 أ + ب) حيث أن أ هما طول الضلعين المتساويين و ب هي قاعدة المثلث.
قد يهمك أيضًا: بحث عن الدوال وأنواعھا كامل