الدالة في الرياضيات هي تعبير أو قاعدة أو قانون تحدد العلاقة بين متغير واحد وهو المتغير المستقل ومتغير آخر وهو المتغير التابع، لذلك فالدوال هي أهم جزء في الرياضيات وهي ضرورية في الفيزياء كذلك. لذلك نقدم لك بحث عن الدوال وأنواعھا كامل للطلاب في المقال التالي فتابع القراءة.
بحث عن الدوال وأنواعھا كامل
الدالة هي عبارة عن علاقة بين مجموعتين من العناصر، المجموعة الأولى تسمى المستقر أما المجموعة الثانية تسمى المنطلق.
فإذا كان المتغير Y من الجموعة الأولى س مرتبطاً بالمتغير x من المجموعة الثانية ص فإنه كلما تم تعيين قيمة عددية لـ x يتم تحديد قيمة فريدة لـ y من خلال قاعدة معينة، ومن ثم يُقال أن y هي دالة للمتغير المستقل x.
يتم ترميز هذه العلاقة بشكل عام كالتالي:
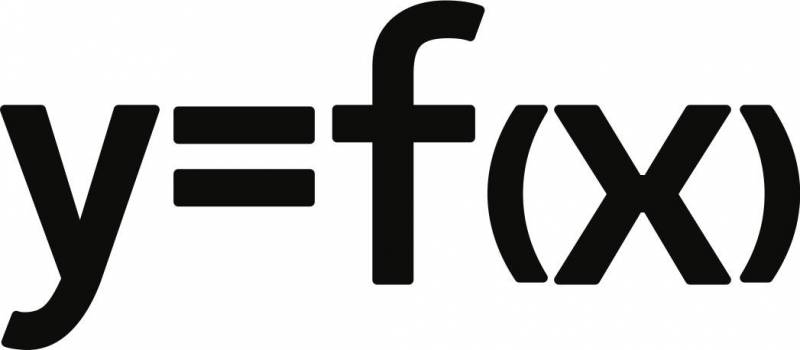
اقرأ أيضاً: كيف تفهم الرياضيات بسهولة
كما أنه غالباً ما تستخدم رموز أخرى بدلاً من f مثل g و p لتمثيل دالة المتغير المستقل x، و خاصةً عندما تكون طبيعة المتغير غير معروفة أو غير محددة.
كذلك كل تابع من المجموعتين يمكنه الارتباط بعناصر المجموعة الأخرى و لكن كل تابع يمكنه الارتباط بعنصر واحد فقط.
أما عناصر مجموعة المستقر فيمكنها الارتباط بجميع عناصر مجموعة المنطلق.
أنواع الدوال
الدالة الثابتة Constant Function
الدالة الثابتة هي دالة خطية يكون فيها التابع ثابت لا تتغير قيمته بغض النظر عن قيمة وسيط الدخل و يتم تمثيلها رياضياص كالتالي .
كما أن مشتق التابع يساوي صفر دائماً فالمشتق هو قيمة التغير للتابع وبما أن التابع لا يتغير فإن المشتق يكون معدوم.
كذلك يتم تمثيل الدالة الثابتة بيانياً على نظام ديكارت بخط مستقيم يوازي محور السينات و يتقاطع مع محور العينات عند قيمة المتغير التابع الثابت.
الدالة المركبة Composition Function
تعتبر الدالة المركبة أحد أشهر أشكال الدوال الرياضية و يكون اقترانها مركب أي أن نتيجة الدالة الأولى تخضع لنتيجة الدالة الثانية.
الدالة التحليلية Analytic Function
في هذه الدالة تكون القيم عقدية و يتم تمثيلها بيانياً بشكل تام و هي متعددة الأنواع و لها أشكال كثيرة من أمثلتها:
- الدوال الابتدائية: و هي لها متغير واحد و يمكن الحصول عليها من خلال عدد معين من العمليات الحسابية.
- متعددة الحدود: يتم حسابها باستخدام الجمع والطرح و الضرب و القسمة و الأسس الصحيحة غير السالبة.
- الدوال الأسية: يتم تمثيلها رياضياً و تستخدم لحساب تعداد السكان و حساب الكتل و الكثافة في الفيزياء.
بالإضافة إلى جميع العمليات الحسابية في مختلف العلوم فهي أسهل أنواع الدوال وتقوم بتسهيل جميع العمليات الحسابية. - الدوال المثلثية: تستخدم في حساب المثلثات ويتم تمثيلها بيانياً حيث تربط نسبة زاوية مثلث قائم مع ضلعين من أضلاعه أي أنها النسبة بين زوايا المثلث القائم.
- اللوغاريتم: وتستخدم هذه الدوال لحساب التطبيقات الهندسية والعلمية وتسمى دوال عكسية لأنها عكس الدوال الأسية.
- دوال الرفع: تنتج دوال الرفع عن ضرب العدد في نفسه أكثر من مرة.
كما تشتهر الدوال التحليلية بأنها يمكن اشتقاقها عدد لا نهائي من المرات.
بالإضافة إلى أن مقلوب الدوال التحليلية لا يساوي صفر في أي نقطة.
الدالة الضمنية Implicit Function
الدالة الضمنية هي دالة متعددة الحدود والمتغيرات ويتم تمثيلها بيانياً بخط منحني يتقاطع مع كل خط عمودي مرة واحدة على الأكثر.
كما أنها مجموع كل النقاط (x ، y) ولكنها تتحول إلى دالة صريحة إذا ظهر المتغير في طرف الدالة وظهر المستقل في الطرف الآخر منها.
اقرأ أيضأً: مفهوم علم الجبر
الدالة الزوجية والفردية Even functions
تستخدم الدوال الزوجية والفردية في التحليل الرياضي ويتم تمثيل الدالة الزوجية رياضياً كالتالي .
لذلك يتم تمثيلها بيانياً تناظرياً أي أن المحور الموجب يكون مماثل للمحور السالب مما يجعلها تشبه الانعكاس فهي تقترن زوجياً.
كذلك الدالة الفردية يتم تمثيلها رياضياً كالتالي حيث تقترن فردياً وليس زوجياً.
وتنتج الدالة الزوجية في الحالات الآتية:
– اقتران الدالة الزوجية مع الدالة الفردية.
– جمع أو طرح دالتين زوجيتين.
– قسمة دالتين زوجيتين.
أما الدالة الفردية فتنتج عند قسمة دالة زوجية على دالة فردية أو قسمة دالة فردية على دالة زوجية.