يهتم علم الطوبولوجيا في الرياضيات، بدراسة خصائص الشكل الهندسي، حيث يتم الحفاظ عليه تحت تشوهات مستمرة، مثل التمدد واللف والتفتت والانحناء، ولكن ليس تمزيقا أو الإلتصاق. لمعرفه المزيد، اليك تعريف علم الطوبولوجيا.
تعريف علم الطوبولوجيا
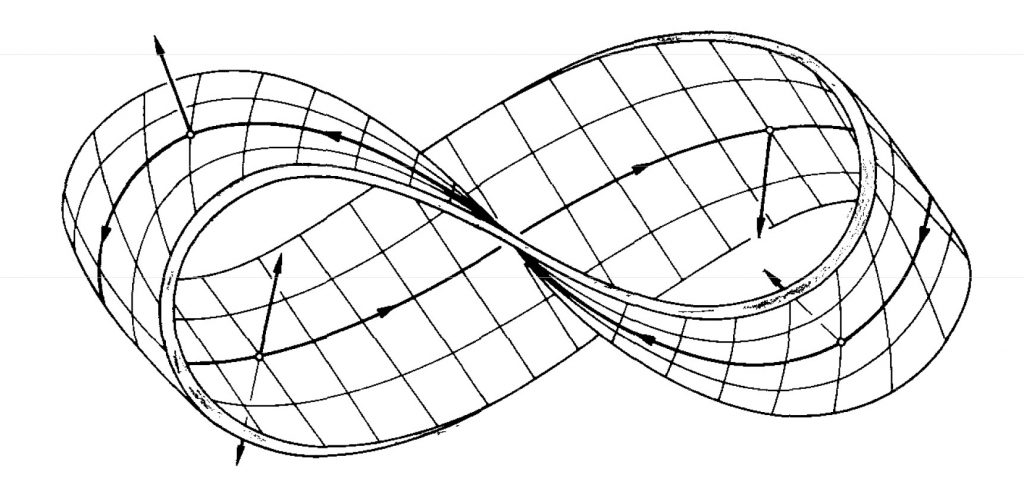
الطوبولوجيا هي فرع جديد نسبيا من الرياضيات، حيث تم إجراء معظم الأبحاث في الطوبولوجيا منذ عام 1900. تهتم بدراسه خصائص المساحات الثابتة تحت أي تشوه مستمر.
يطلق علي الطوبولوجيا أحيانا اسم هندسة الألواح المطاطية لأنه يمكن تمديد الكائنات وتقليصها مثل المطاط، ولكن لا يمكن كسرها او تمزيقها. على سبيل المثال، يمكن تشويه مربع في دائرة دون كسرها، فإن المربع مكافئ من الناحية الطوبولوجية للدائرة ، ولكنه يختلف عنها.
تتمثل النظرة المحفزة وراء الطوبولوجيا في أن بعض المشكلات الهندسية لا تعتمد على الشكل الدقيق للأشياء المعنية، بل تعتمد على طريقة تجميعها على سبيل المثال، يكون للميدان والدائرة العديد من الخصائص المشتركة: كلاهما ذو بعد واحد من وجهة نظر طوبولوجية وكلاهما يفصل المستوى إلى قسمين.
تستخدم الطوبولوجيا في العديد من فروع الرياضيات، مثل المعادلات المختلفة، الأنظمة الديناميكية، نظرية العقد، وأسطح ريمان في التحليل المعقد، كما أنها تستخدم في نظرية الأوتار في الفيزياء، ولتوصيف بنية الفضاء الزماني للكون.
انواع الطوبولوجيا
يوجد العديد من الحقول الفرعية للطبولوجيا فيما يلي شرح لبعضها:
طوبولوجيا عامة أو نقطة طوبولوجيا
الطوبولوجيا العامة عادة ما تأخذ في الاعتبار الخصائص المحلية للمسافات، وترتبط ارتباطا وثيقًا بالتحليل، إنه يعمم مفهوم الاستمرارية لتحديد المساحات الطوبوغرافية، والتي يمكن فيها النظر في حدود التسلسل.
يمكن تعريف المسافات في بعض الأحيان بالمساحات، وفي هذه الحالة تسمى المسافات المترية، مما يعنى مفهوم المسافة المنطقي.
طوبولوجيا اندماجي
تأخذ طوبولوجيا التوافقية في الاعتبار الخصائص العالمية للمسافات، التي تم إنشاؤها من شبكة من الرؤوس والحواف والوجوه، هذا هو أقدم فرع من الطوبولوجيا، ويعود تاريخه إلى أويلر.
حيث اثبت أن المساحات المكافئة طبولوجيا لها نفس العدد الثابت، والذي نسميه الآن خاصية أويلر، هذا هو الرقم (V – E + F)، حيث V و E و F هي عدد الرؤوس والحواف ووجوه الكائن. على سبيل المثال، فإن رباعي الاسطح والمكعب يعادلان طبولوجيا إلى كرة، وأي ميزة تثليث للكرة لها خاصية أويلر 2.
الطوبولوجيا الجبرية
تتناول طوبولوجيا الجبر الخصائص العالمية للمسافات، وتستخدم كائنات جبرية مثل المجموعات والحلقات للإجابة على الأسئلة الطوبولوجية.
طوبولوجيا الجبر يحول المشكلة الطوبولوجية إلى مشكلة جبرية يسهل حلها، على سبيل المثال، يمكن ربط مجموعة تدعى مجموعة متجانسة بكل مساحة، ويمكن التمييز بين الزجاجة وزجاجة كلاين بسبب وجود مجموعات تماثل مختلفة.
تستخدم طوبولوجيا الجبر أحيانا التركيب التوافقي لمسافة لحساب المجموعات المختلفة المرتبطة بذلك الفضاء.
الطوبولوجيا التفاضلية
يعتبر الهيكل التفاضلي المساحات ذات نوع من النعومة المرتبطة بكل نقطة، في هذه الحالة، لن يكون المربع والدائرة متساويان أو مختلفان مع بعضهما البعض.
تعتبر الطوبولوجيا التفاضلية مفيدة لدراسة خصائص حقول المتجهات، مثل الحقول المغناطيسية أو الكهربائية.
المراجع